官方发布2022年重庆市考笔试通知了吗_2022年重庆省考延期多久

【导读】重庆华图为您提供：官方发布2022年重庆市考笔试通知了吗_2022年重庆省考延期多久，详细信息请阅读下文！如有疑问请点【重庆华图咨询平台】，更多资讯请关注重庆华图微信公众号(CQhuatu)，重庆华图咨询电话：023-67518090。

　　【重启预约】2022重庆公务员笔试成绩时间有奖竞猜：点击进入

　　2022年省考笔试终于有官方消息了，笔试真的不远了!!!，由河南公务员考试网发布了一则通知关于做好考试疫情防控的公告本以为是跟高考息息相关，但是官方特地标注(省直考区)这样一来，事情就不再简单起来?

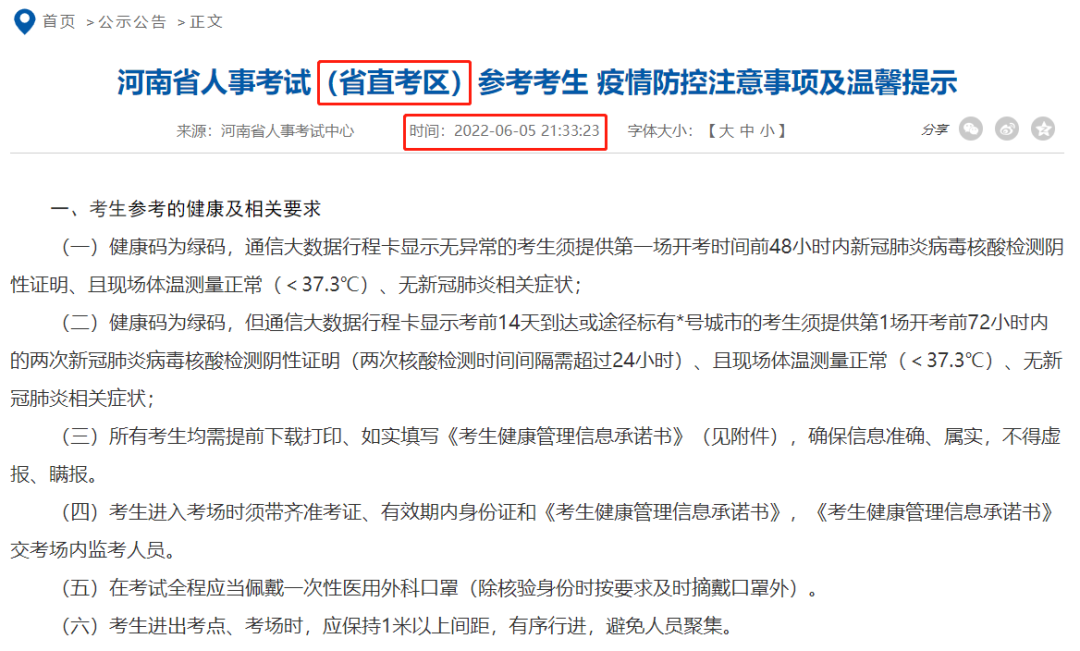
　　内容大概是考生的健康要求，如果只是这样，还不足以让大家提起第一戒备，之后，河南又悄悄更新了省考打印入口，虽然没有具体的准考证打印时间，但是看起来是真的快了

　　同时，西藏公务员笔试时间也正式确认西藏省考公告是3月16日发布的，虽然西藏不参加省联考，但是笔试消息确定无疑是一个重大信息，笔试定于7月9日

　　这就意味着省考马上重启了，7月初可能就要恢复大规模联考，算一算时间也差不多了，现在上海重启，北京恢复正常，各地疫情都已经好转，而且高考已经结束了，你觉得省联考会在7月9日笔试吗?

　　笔试时间暂未确定，备考一定不要停，小编给大家分享一些备考热点，希望可以帮助备考的小伙伴们!

—— 重庆公务员备考 ——

2022重庆公务员考试数量关系备考冲刺：牛吃草问题

　　牛吃草问题是公考数量中一种非常典型的问题。由于其特征明显、公式简单，因此这一题型是考生拿分的重要题型。但也由于其过于简单，近年来公考中牛吃草问题不再是常客。实际上在整个公考数量中，牛吃草问题仍占有一席之地，只不过考查的方式变得多种多样，更侧重于对公式的理解，而非使用。

　　牛吃草的本质是行程问题中的追及问题，可以想象成草以一定的速度在生长，牛以更快的速度在吃草，牛吃草总量=原有草量+新增草量。其中，牛吃草的总量等于牛吃草的速度乘以牛吃草的时间;新增草量等于草的生长速度乘以草的生长时间。因此套用行程问题中的追及公式，也就得到了牛吃草问题的核心解法：y=(N-x)×T。

　　这个公式中，y代表原有草量、N代表牛的头数、x代表草的增速、T代表时间。隐含的假设为每头牛每天的吃草量为1(即牛吃草速度)。

　　牛吃草典型的考法有抽水机抽水、检票口检票、资源开采等。而牛吃草的特征也非常的明显，题干中出现排比句，类似于N1数量……需要T1时间;N2数量……需要T2时间……就可以判断为牛吃草问题。

　　先来看一道简单的牛吃草问题。

　　【例1】有一个水池，池底不断有泉水涌出，且每小时涌出的水量相同。现要把水池里的水抽干，若用5台抽水机40小时可以抽完，若用10台抽水机15小时可以抽完。现在用14台抽水机，多少小时可以把水抽完?

　　A.10小时 B.9小时

　　C.8小时 D.7小时

　　【答案】A

　　【解析】第一步，本题考查牛吃草问题，用方程法解题。

　　第二步，设水池里的水量为y，每小时涌出的水量为x，根据40小时抽完可得y=(5-x)×40，根据15小时抽完可得y=(10-x)×15，解得x=2，y=120。

　　第三步，设使用14台抽水机抽完水需要时间为t小时，则120=(14-2)×t，解得t=10。

　　因此，选择A选项。

　　此题中，“若用……若用”的排比句结构非常明显，直接代入公式解方程即可得到答案。然而这种考查方式已经很少见到，目前考查的牛吃草问题，往往需要首先判断哪一个量是草，哪一个量又是牛。一般来说，以恒定的速度一直在增加或消耗，就是草，它的速度即是x。

　　【例2】由于连日暴雨，某水库水位急剧上升，逼近警戒水位。假设每天降雨量一致，若打开2个水闸放水，则3天后正好到达警戒水位;若打开3个水闸放水，则4天后正好到达警戒水位。气象台预报，大雨还将持续七天，流入水库的水量将比之前多20%。若不考虑水的蒸发、渗透和流失，则至少打开几个水闸，才能保证接下来的七天都不会到达警戒水位?

　　A.5 B.6

　　C.7 D.8

　　【答案】B

　　【解析】第一步，本题考查牛吃草问题。

　　第二步，假设原水位与警戒水位之间相差的蓄水量为y，每天流入水库的水量为x，由正好到达警戒水位得y=(x-2)×3，y=(x-3)×4，解得x=6，y=12。

　　第三步，由比之前多20%，可知现在每天流入水库的水量为6×(1+20%)=7.2。设至少打开N个水闸，可得12=(7.2-N)×7，解得N≈5.5，故至少打开6个水闸。

　　因此，选择B选项。

　　这道牛吃草问题不但需要根据“每天降雨量一致”来判断降雨量是草，还有一个典型的特征就是草的速度后期发生了变化，这也是近几年牛吃草问题的新特征——“草”的速度可能会变化、“牛”的头数也可能会变化;或者牛没有吃完，即草存量发生变化。但只要考生理解公式的核心概念，抓住公式的本质进行求解，牛吃草问题仍然是我们拿分的一种简单题型。

　　【例3】某河道由于淤泥堆积影响到船只航行安全，现由工程队使用挖沙机进行清淤工作，清淤时上游河水又会带来新的泥沙。若使用1台挖沙机300天可完成清淤工作，使用2台挖沙机100天可完成清淤工作。为了尽快让河道恢复使用，上级部门要求工程队25天内完成河道的全部清淤工作，那么工程队至少要有多少台挖沙机同时工作?

　　A.4 B.5

　　C.6 D.7

　　【答案】D

　　【解析】第一步，本题考查牛吃草问题。

　　第二步，设河道原来的淤泥堆积量为y，每天上游河水带来新的淤泥量为x，根据牛吃草问题公式：y=(N-x)×T，可列方程组：y=(1-x)×300，y=(2-x)×100。解得x=0.5，y=150。

　　第三步，设要想25天内完成清淤工作至少需要n台挖沙机，可列方程：150=(n-0.5)×25，解得n=6.5，即至少需要7台挖沙机。

　　因此，选择D选项。

　　通过这几道题目考生可以发现，牛吃草问题万变不离其宗，本质是：①掌握牛吃草问题的核心概念，②灵活使用公式进行求解，③如果遇见分数小数要知道求整的方向。如果能做到这3点，牛吃草问题必将成为考生拿分的囊中之题。