2022年重庆市公务员考试准考证打印网址_2022重庆省考笔试恢复时间

【导读】重庆华图为您提供：2022年重庆市公务员考试准考证打印网址_2022重庆省考笔试恢复时间，详细信息请阅读下文！如有疑问请点【重庆华图咨询平台】，更多资讯请关注重庆华图微信公众号(CQhuatu)，重庆华图咨询电话：023-67518090。

　　关于恢复举行重庆市2022年度公开考试录用公务员笔试的公告

　　经研究，决定于2022年7月9日、10日恢复举行重庆市2022年度公开考试录用公务员笔试。考试科目及内容不变，具体考试时间及地点详见准考证。考生请于2022年7月5日上午9:00至7月10日上午10:00期间，登录报名网站打印准考证。如遇问题，请拨打网上报名技术咨询电话(023—86868837、023—86868838)。

　　为保障广大考生生命安全和身体健康，请考生按照要求填报本人考前14天内居住地详细地址(具体要求详见附件)。另外，市人事考试中心将于6月下旬在重庆市人力资源和社会保障局网站，发布《重庆市2022年度公开考试录用公务员笔试应试人员疫情防控须知》。请广大考生按照疫情防控相关要求，合理安排时间，提前做好相应准备，避免影响参加考试。

　　感谢广大考生的理解、支持和配合。

　　附件：关于完善重庆市2022年度公开考试录用公务员考试考生个人信息的通告

　　重庆市公务员局

　　2022年6月13日

　　附件

关于完善重庆市2022年度公开考试录用公务员考试考生个人信息的通告

　　为严格贯彻落实新冠肺炎疫情防控有关要求，全力保障考生健康安全，根据当前疫情防控工作需要，现就相关事项通告如下：

　　一、请考生于6月15日9:00至6月19日18:00期间，登录http://ggfw.rlsbj.cq.gov.cn/wsbm/wsbm_cqpta/index.html#/index，选择重庆市2022年度公开考试录用公务员考试项目，如实填报本人考前14天内居住地详细地址等相应信息，逾期未填报的，后期可能会影响正常参考。

　　二、凡隐瞒或谎报现居住地、旅居史、接触史、健康状况等疫情防控重点信息，不配合工作人员进行防疫检测、询问等造成不良后果的，取消考试资格;如有违法情况，将依法追究法律责任。

　　点击查看：2022全国公务员联考笔试重启时间汇总

>>>购买入口：2022重庆公务员招录考试考前冲刺试卷<<<

—— 重庆公务员备考 ——

2022重庆公务员考试数量关系备考：排列组合去重复

　　排列组合去重复

　　众所周知，重复计数是排列组合问题的主要错误之一，而此类问题具有隐蔽性，不易被发现。本文就排列组合中几种常见的重复性错误加以剖析，来提升大家解决问题的能力。

　　排列组合问题中一个核心的要素是不重不漏，那如何才能避免重复计数呢，这就需要我们了解重复产生的原因。常见的容易产生重复的情况主要有三类：第一，分步引起重复计算;第二，平均分组易重复计算;第三，环形排列易重复计算，这里我们先介绍前两类：

　　一、分步引起重复计算

　　【例】从5名男生5名女生中选出4人，去参加培训，在选出的4人中至少有1名男生1名女生的情况数有多少种?

　　共50+100+50=200种。

　　类似的题目在公考中屡见不鲜，下面就通过两道题目对比理解：

　　【例1】在九宫格内依次填入数字1—9，现从中任取两个数，要求取出的两个数既不在同一行也不在同一列，共有多少种不同取法?

　　A.9

　　B.18

　　C.36

　　D.45

　　【答案】B

　　【解析】

　　第一步，本题考查排列组合问题，属于基础排列组合。

　　因此，选择B选项。

　　【例2】在7×7的队列中，先随机给一个队员戴上红绶带，再给另一个队员戴上蓝绶带，要求戴两种颜色绶带的这两位队员不在同一行也不在同一列。问有多少种戴法?

　　A.1048

　　B.1374

　　C.1764

　　D.1858

　　【答案】C

　　二.平均分组易重复计算

　　【例】将6个人平均分成3组，每组2人，有多少种分组方式?

　　下面通过几道公考题目加深理解：

　　【例3】将10名运动员平均分成两组进行对抗赛，问有多少种不同的分法?

　　A.120

　　B.126

　　C.240

　　D.252

　　【答案】B

　　【解析】

　　第一步，本题考查排列组合问题，属于基础排列组合。

　　【例4】某班共有8名战士，现在从中挑出4人平均分成两个战斗小组分别参加射击和格斗考核，问共有多少种不同的方案?

　　A.210

　　B.420

　　C.630

　　D.840

　　【答案】B

　　【解析】

　　第一步，本题考查排列组合问题，属于基础排列组合。

　　因此，选择B选项。

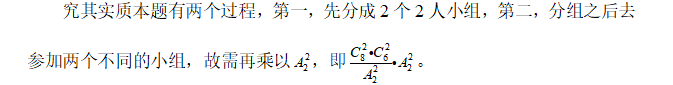
　　【例5】某单位组织志愿者参加公益活动，有8名员工报名，其中2名超过50岁。现将他们分成3组，人数为3、3、2，要求2名超过50岁的员工不在同组，则不同分组的方案共有：

　　A.120种

　　B.150种

　　C.160种

　　D.210种

　　【答案】D

　　【解析】

　　第一步，本题考查排列组合问题，属于基础排列组合。

　　第二步，根据要求2名超过50岁的员工不在同组，有以下2种情况：

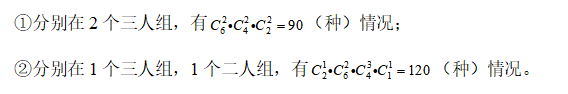
　　第三步，不同分组的方案共有90+120=210(种)。

　　因此，选择D选项。

　　例5是平均分组中较难的综合题目，但你只要明白了平均分组本质及原理，本题也会迎刃而解。

（编辑：bailin01）