2024重庆事业单位11月2日联考准考证打印入口_重庆事业单位考试

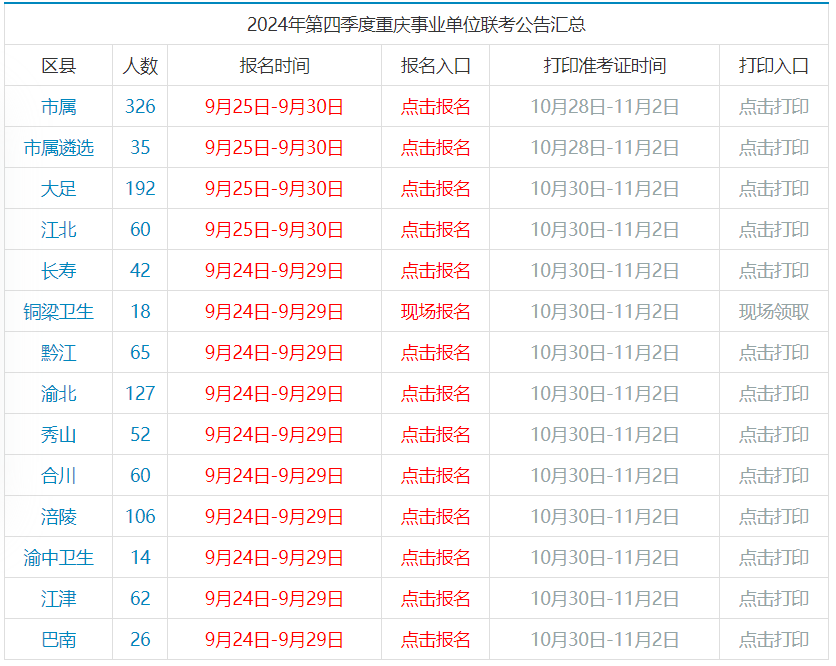
点击打印：2024年重庆事业单位11月2日准考证打印入口汇总

点击查看：2024年重庆事业单位11月2日联考报名统计

扫一扫，咨询重庆事业单位考试备考资料，附件下载 疑问解答

免费领取，重庆事业单位ABCE类笔试备考资料

　　重庆1102事业单位联考公告!你是不是还不清楚自己该备考哪一类?图图就来给大家详细讲讲各类的区别。注意，以下内容仅供参考，最终备考内容以实际岗位表上面的类别为主!

　　01、综合管理类(A类)

　　适用于

　　事业单位中以行政性、事务性和业务管理为主的岗位。

　　招聘专业主要有

　　工商管理类、法律类、中国语言文学类、经济学类、汉语言文学类、会计与审计类、新闻传播学类、财务管理类、计算机科学与技术、电子商务、工商管理及市场营销、工业工程、公共管理、管理科学与工程、旅游管理、农林管理、物流管理与工程、财政税务、金融、经济贸易与管理、人力资源管理、安全生产、材料学、计算机、统计学、专业不限等。

　　笔试内容

　　《职业能力倾向测验(A类)》分为：常识判断+言语理解与表达+数量关系+判断推理+资料分析，各科目分值共150分。

　　《综合应用能力(A类)》试卷由注意事项、背景材料和试题三部分组成，全部是主观性试题。试题内容主要涉及事业单位管理岗位典型的工作任务，如观点归纳、资料分类、草拟信函、会务安排、应急处理、联络通知等。主要为案例分析题和应用文写作题两大类型。

　　02、社会科学专技类(B类)

　　适用于

　　事业单位人文社科类专业技术岗位。比如经济、新闻、出版编辑、公证员、馆员、会计、广电播音、工艺美术等岗位。

　　招聘专业主要有

　　会计学、体育学、教育学、历史学、外国语言文学、新闻出版、数字媒体艺术等相关专业、哲学、中国语言文学、美术及摄影、设计学、舞蹈学、戏剧与影视、艺术理论、音乐学、法学、民族学、社会学、政治学类、马克思主义理论类等。

　　笔试内容

　　《职业能力倾向测验(B类)》分为：常识判断+言语运用+数量分析+判断推理+综合分析，各科目分值共150分。

　　《综合应用能力(B类)》试卷由主观性试题组成，主要题型包括概念分析题、校阅改错题、论证评价题、材料分析题和写作题等。每次考试从上述题型中组合选用。

　　03、自然科学专技类(C类)

　　适用于

　　事业单位自然科学类专业技术岗位。比如工程、农技、统计、民航飞行、关务员、实验员、技工学校教师等岗位。

　　招聘专业主要有

　　计算机科学与技术、水利水电工程、植物生产类、土木工程、土木类、农业工程类、化学类、机械设计制造及其自动化、建筑学、农学、农业技术类、大气科学类、机械类、水利类、生物学、食品科学及工程、数学、水利水电水工、天文及大气科学、统计学、物理学、公安技术等。

　　笔试内容

　　《职业能力倾向测验(C类)》分为：常识判断+言语运用+数量分析+判断推理+综合分析，各科目分值共150分。

　　《综合应用能力(C类)》试卷以主观性试题为主，主要题型包括科技文献阅读题、论证评价题、科技实务题、材料作文题等。每次考试从上述题型中组合选用。

　　04、中小学教师类(D类)

　　适用于

　　中小学(含幼儿园)和中专等教育机构的教师岗位。

　　笔试内容

　　《职业能力倾向测验(D类)》分为：言语理解与表达+数量分析+判断推理类比推理+策略选择，各科目分值共150分。

　　《综合应用能力(D类)》试卷主要题型包括辨析题、案例分析题、教育方案设计题等，旨在测查应试人员综合运用教育学、心理学等相关知识和技能，分析、解决中小学教育教学问题的能力。

　　05、医疗卫生类(E类)

　　适用于

　　医疗卫生机构专业技术岗位。比如临床、护理、放射师等岗位。

　　招聘专业主要有

　　基础医学类、预防医学类、卫生管理类、临床医学类、医学技术类、口腔医学类、中医学类、护理学类、药学类等。

　　笔试内容

　　《职业能力倾向测验(E类)》包括常识判断、言语理解与表达、数量分析、判断推理、策略选择等部分。

　　《综合应用能力(E类)》试卷主要由医学基础知识和招聘岗位专业知识应用能力两个部分组成。其中，医学基础知识部分占比60%，所有应试人员必答;招聘岗位专业知识应用能力部分占比40%，具体分为中医临床、西医临床、药剂、护理、医学技术、公共卫生管理六个类别，应试人员应根据报考岗位选做相应类别的试题。

　　目前，重庆1102事业单位联考公告陆续发布中，明日将开启报名入口，大家可以具体查看职位表里面的类别，还没有心仪岗位，仍在等公告的同学可以先参考上文内容选择对应的类别来备考。

　　重庆事业单位职业能力倾向测验：完全平方数的约数

　　约数倍数问题是数量关系模块中一类非常重要的题型，而完全平方数的约数个数又是约数倍数问题里面经常会考到的一个知识点，今天华图教育带大家一起来认识一下平方数的约数。

　　判断一个数的约数个数时，我们往往先将这个数进行质因数分解，然后把各个质因数的幂次数字分别加1，最后再相乘，得到的数字就是这个数的约数个数。其中最小的约数是1，最大的约数是这个数字本身。例如：，那么120的约数个数一共有(3+1)X(1+1)X(1+1)=16(个)。

　　在实际做题过程中，有一类题型考察的本质往往是让我们判断一个数的约数个数是奇数还是偶数，根据上述规律可知，想让一个数的约数个数是奇数，那么对其进行质因数分解后其所有质因数的指数应该都是偶数(因为一旦有一个指数是奇数，加1之后就是偶数，最后乘出来的总约数个数必然是偶数)，而满足此条件的数只能是完全平方数。因此我们可以总结规律：若一个数的约数个数是奇数，那么这个数一定是完全平方数。

　　一、例题精讲

　　【例1】设有编号为1、2、3…10的10张背面向上的纸牌，现有10名游戏者，第1名游戏者将所有编号是1的倍数的纸牌翻成另一面向上的状态，接着第2名游戏者将所有编号是2的倍数的纸牌翻成另一面向上的状态，……，第n名(n≤10)游戏者，将所有编号是n的倍数的纸牌翻成另一面向上的状态，如此下去，当第10名游戏者翻完纸牌后，那些纸牌正面向上的最大编号与最小编号的差是( )。

　　A. 2

　　B. 4

　　C. 6

　　D. 8

　　【答案】D

　　【解析】首先我们根据题目中所说的翻牌规律确定一下纸牌被翻的次数由什么决定：

　　比如编号为6这张纸牌在这个过程中会被第1名，第2名，第3名，第6名，各翻1次，一共被翻了4次，而1、2、3、6正好是6的4个约数，因此我们知道纸牌被翻的次数等于其编号的约数个数。刚开始纸牌都是背面朝上，而题目问题是最终正面朝上的纸牌最大编号与最小编号差，故最终想让纸牌正面朝上，这张纸牌在整个过程中应该被翻了奇数次，即这张纸牌的编号的约数个数应该是奇数。一个数的约数个数是奇数，那么这个数一定是完全平方数，1~10之间只有1、4、9这3个数字是完全平方数，那么最大和最小的编号之差为9-1=8，故选D。

　　【例2】编号为1—50的选手参加一个爬楼比赛，楼高为60层，所有选手在第1层均获得一个特别的号牌，此后每经过一个楼层，如果选手的编号正好是楼层数的整数倍，就将得到一个特别的号牌，所有选手都到达终点后，正好持有3个特别号牌的选手有多少人?

　　A. 1

　　B. 4

　　C. 7

　　D. 10

　　【答案】B

　　【解析】首先我们根据题目中的规律来探索一下选手最终持有的的特别号牌数量与选手编号的关系：例如编号为8的选手会在第1层，第2层，第4层，第8层各获得一个特别号牌，共获得4个特别号牌。而1、2、4、8正是编号8的4个约数，因此我们知道选手最终获得特别号牌的个数就是其本身编号的约数个数。题目中说正好持有3个特别号牌，说明选手的编号一共有3个约数。3为奇数，说明选手编号一定是完全平方数，即编号可以表示为a2这样的形势，而只有当a为质数的时候才能保证恰好有3个约数，在1-50中，满足条件的有22、32、52、72，一共4个，所以选B。

　　总之，一个数的约数个数若为奇数个，那么这个数必是完全平方数，牢牢把握这一规律，我们才能在较短的时间内选出正确的答案。

　　原文标题：事业单位职业能力倾向测验：完全平方数的约数

　　文章来源：华图教育(MD5：4fe2ccf091fdf50a133406bd99028332)