2022国考第三天报报名人数是多少_国家公务员报名入口已开通

【导读】重庆华图为您提供：2022国考第三天报报名人数是多少_国家公务员报名入口已开通，详细信息请阅读下文！如有疑问请点【重庆华图咨询平台】，更多资讯请关注重庆华图微信公众号(CQhuatu)，重庆华图咨询电话：023-67518090。

　　2022国家公务员考试报名入口已开通，报名时间为2022年10月15日至10月24日，报名时间一共10天，建议各位考生要抓紧时间进行报名。请收藏本站，届时重庆华图教育将会及时同步更新：

报名入口：2022国家公务员考试报名入口(10月15日-10月24日)

　　网上报名

　　本次招考主要采取网上报名方式，按照以下程序进行：

　　1. 提交报考申请。报考者可于2021年10月15日8:00至10月24日18:00期间登录考录专题网站进行报名并提交报考申请，每次只能选报1个职位。报名时，应当仔细阅读诚信承诺书，提交的报考申请材料应当真实、准确、完整。报考者提供虚假报考申请材料的，一经查实，将取消报考资格，涉及伪造、变造有关证件、材料、信息骗取考试资格的，将按有关规定严肃处理。

　　2. 查询资格审查结果。报考者可于2021年10月15日至10月26日期间登录考录专题网站查询资格审查结果。通过资格审查的，不能再报考其他职位。2021年10月15日8:00至10月24日18:00期间，报考申请未审查或者未通过资格审查的，可以改报其他职位。2021年10月24日18:00以后，报考申请未审查或者未通过资格审查的，不能再改报其他职位。

　　资格审查贯穿招考全过程。在招考各环节发现报考者不符合报考资格条件的，招录机关均可取消其报考资格或者录用资格。

　　3. 查询报名序号。通过资格审查的报考者，可于2021年10月28日8:00后登录考录专题网站查询报名序号，报名确认和下载打印准考证时需提供该序号，请务必牢记。

　　(三)报名确认

　　通过资格审查的报考者，可于2021年11月1日0:00至11月7日 24:00登录考录专题网站进行网上报名确认并缴费。逾期未完成网上报名确认并缴费的，视为自动放弃报考资格。

　　最低生活保障家庭人员可以直接与当地考试机构联系办理报名确认和减免费用手续。各省(自治区、直辖市)考试机构的咨询电话将于2021年10月31日以后通过考录专题网站公布。

　　(四)网上打印准考证

　　报名确认成功的报考者，请于2021年11月22日0:00至11月28日12:00期间登录考录专题网站打印准考证。如遇问题，请与当地考试机构联系解决。

>>>点击入口：2022年国家公务员报名统计<<<

---

　　2022国家公务员考试招录公告已发布，为帮助考生朋友们尽快了解国家公务员考试公告详情，重庆人事考试网特为大家提前整理了2022国家公务员考试招录公告信息汇总，方便大家查看。重庆小编还提供了国家公务员职位表、报名入口、缴费入口，准考证打印入口等内容，祝大家考试顺利!

2022国家公务员考试招录公告公告信息汇总
考试公告	2022国家公务员考试招录公告公告
职位表	2022国家公务员考试招录公告职位表（全国）
	2022国家公务员考试招录公告职位表（重庆）
报考指南	2022国家公务员考试报考指南
报名入口	2022国家公务员考试招录公告报名入口（10月15日-10月24日）
缴费入口	2022国家公务员考试缴费入口（11月1日-11月7日）
准考证打印入口	2022国家公务员考试准考证打印入口（11月22日-11月28日）
报名统计	2022国家公务员考试报名统计
报名推荐表/登记表	2022国家公务员考试报名推荐表/登记表下载
考试大纲	2022国家公务员考试大纲
考试内容	2022国家公务员考试内容
笔试成绩	2022国家公务员考试笔试成绩查询入口（2022年1月）
报考条件	2022国家公务员考试招录公告考试报名条件有哪些
公告峰会	2022国家公务员考试招录公告解读峰会
笔试课程	2022国家公务员考试笔试辅导课程

　　我是新手，怎么备考2022国考：

　　对考生来说，一定要做好时间规划，才能对考试做全面的复习。

　　1.基础学习——确立科目知识理论框架，扎实技巧方法

　　对于很多考生而言，公考的考试科目知识都是第一次接触，这种情况下首先应该梳理基本的学科知识树，确立科目知识理论框架。

　　在学习基础知识时，可以选择基础理论书籍，比如侧重不同考情，梳理基础知识理论框架的各省公务员考试教材或《国家公务员录用考试专用教材》，也可以选择对知识理论细节挖掘更为深入的知识理论书籍，比如《模块宝典》《申论万能宝典》等。

　　在学习的过程中，切忌只学理论，不做题目。正所谓“光说不练假把式”，任何技巧不经过练习都没有办法在考试中发挥作用。

　　在学习理论的过程中，一定要学一个知识点，对应练习一组题。大家在选择题目的时候，一定要选择区分难易程度的分科目分技巧的题册。只有这样才能起到针对性练习，扎实技巧方法的作用。

　　2.强化学习——巩固知识理论，查漏补缺知识方法技巧

　　建构了知识体系之后，要通过练习稍有难度的题目，检测学到的技巧方法掌握是否扎实。这个阶段，大家可以使用之前购买的题册，练习每个方法中对应的强化难度或中等难度的题目，根据练习自测情况找出自己掌握比较薄弱的技巧方法，重新学习巩固，这样就能起到查漏补缺的作用。

　　3.题海学习——了解考情趋势，预演考试提高做题效率

　　查漏补缺之后，我们对知识的掌握就基本过关了。这时建议大家准备好所有参加考试的历年真题，从最近的真题做起，了解考情趋势。我们要通过套题练习分析考试趋势与该考试的特色考情，根据近几年考试的重点明确后期复习巩固的侧重点。另外，也要通过这些真题的练习习惯考试当时的场景、节奏，提高做题的效率。

　　4.冲刺复习—全真模拟考试，预测练习提前适应考试。

　　在距离考试一到两周的时候，应该开始完全按照考试的时间自己安排全真模考，用对应考试的预测试卷或密卷进行练习。一方面，这能起到预测作用，另一方面，这也能让我们提前找到考试的感觉，真正进入考场时，就不那么容易紧张。

　　另外，这里图图提到一个小技巧——当考试真题不好找时，我们可以从预测试卷或密卷入手，去研究考试的出题情况。因为这类试卷的仿真程度很高，对于指导我们备考有非常重要的作用。比如近期要考试的军队文职，其中的专业科目考试试题在市面上非常难找，要做好准备，可以去找军队文职考前专业科目密押卷，了解科目的命题情况。

　　5.阶段模考—自测把握方向

　　阶段模考并不是最终阶段才要做的工作，而是每进行一个阶段的学习后应该去做的工作，经过阶段检测，我们才知道自己一个阶段的学习情况如何，下一个阶段应该往哪个方向努力。如果觉得自己进行分析自测不够准确，可以选择购买测评，专业的批改和分析报告对于下一步备考指导意义更大。

　　以上备考五条，1-3阶段的时间要根据整体时间自行安排。总之，开始得越早，时间安排灵活度越高。

—— 国家公务员备考 ——

2022年国家公务员行测数量关系备考干货之奇偶特性的妙用

　　奇偶特性是较常见的一类整数特性，在解题过程中我们往往并不会应用奇偶特性直接解题，而是与代入排除结合使用，可以大大加快我们的解题速度。

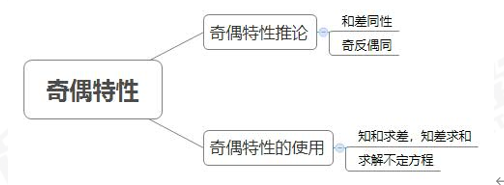
　　一、奇偶特性及其推论：

　　首先我们要了解一下下面几个等式：

　　奇数±奇数=偶数;偶数±偶数=偶数;奇数±偶数=奇数。

　　通过观察以上加减法的等式，我们不难发现以下两个推论：

　　1.和差同性：两个数做和，如果结果是奇数，那么做差的结果也是奇数。如果做和结果是偶数，那么做差的结果也是偶数;

　　2.奇反偶同：如果两个数做和或者差的结果为奇数，那么这两个数一定是性质相反，即为一个奇数和一个偶数。如果两个数做和或者做差的结果为偶数，那么这两个数一定是同为奇数或同为偶数。

　　二、奇偶特性的应用：

　　1.知和求差，知差求和：当我们已知两个数的和，求两个数的差;或已知两个数的差，求两个数的和时，可以利用“和差同性”这个推论。结合代入排除，可以大大加快解题速度。

　　2.解不定方程：当遇到不定方程中的未知数系数出现偶数时，可以考虑使用“奇反偶同”这个推论来求解不定方程。

　　三、实战演练：

　　例1.四年级有4个班，不算甲班其余三个班的总人数是131人;不算丁班其余三个班的总人数是134人;乙、丙两班的总人数比甲、丁两班的总人数少1人，问这四个班共有多少人?

　　A. 177

　　B. 178

　　C. 264

　　D. 265

　　【思路点拨】本题正确答案为A选项。设甲、乙、丙、丁四个班人数分别为a、b、c、d，则所求为a+b+c+d的量。根据第二个条件可知(a+d)-(b+c)=1是一个奇数;我们把(a+d)和(b+c)分别看成两个整体，根据奇偶特性的推论“和差同性”可知(a+d)+(b+c)一定是一个奇数，因此我们所求的四个班级的人数和一定是奇数。可以排除B、C两个选项。剩余的两个选项我们只需要稍加分析即可，根据题干前半部分可知b+c+d=131，a+b+c=134，两个等式相加才等于265，大于四个班级人数的和。所以 排除D选项。因此，选择A选项。

　　例2.某儿童艺术培训中心有5名钢琴教师和6名拉丁舞教师，培训中心将所有的钢琴学员和拉丁舞学员共76人分别平均地分给各个老师带领，刚好能够分完，且每位老师所带的学生数量都是质数。后来由于学生人数减少，培训中心只保留了4名钢琴教师和3名拉丁舞教师，但每名教师所带的学生数量不变，那么目前培训中心还剩下学员多少人?

　　A. 36

　　B. 37

　　C. 39

　　D. 41

　　【思路点拨】本题正确答案为D选项。设每名钢琴、拉丁舞老师分别带领学员x、y人，由共76人，可列不定方程5x+6y=76。两个量的和为偶数，根据奇偶特性的推论“奇反偶同”可以推出5x、6y的奇偶性相同，而6y是6的倍数，一定是偶数，所以5x一定是偶数，故x为偶数。根据题干条件可知x也为质数，而2是唯一的偶质数，所以x=2，代入方程后可得y=11，即每名钢琴老师带2名学员，每名拉丁舞老师带11名学员。由所带学生数不变可得，剩余学员有4×2+3×11=41(人)。

　　好了，不知道小伙伴们是否学会了呢，奇偶特性在解题时对于我们提升做题速度往往有着巨大的作用，稍加练习就会熟练了哦!

　　来源文章：重庆分院

（编辑：bailin01）