2023重庆公务员行测数量关系之不定方程破解之法

【导读】重庆华图为您提供：2023重庆公务员行测数量关系之不定方程破解之法，详细信息请阅读下文！如有疑问请加【2022重庆公务员考试交流群:677564082】 ，更多重庆公务员备考指导/技巧/试题请关注重庆华图微信公众号CQhuatu，重庆华图咨询电话：023-67518090。

推荐：2022版重庆公务员6本套（教材+历年+同步练习册）

推荐：2022版华图公务员考试 内部教案 12本套

　　行测备考中数量关系模块很重要，且它也让我们很头痛，因为它确实有一定难度。也就是因为它的难，也让很多同学望而却步，错失了拿分的机会，所以，我们更要迎难而上，掌握科学的方法，既快又准的解决难题。本次就给大家介绍不定方程的破解之法，帮助大家更好的解题。

　　何为不定方程?即未知数个数大于方程式个数。比如，5x+6y=18。也就是因为未知数多于方程式个数，所以很难直接解方程得出结果。主要是因为给的条件太少，所以如果想要解出符合题目的答案，要给方程式补条件，如何补?一是结合选项代入排除，二是考虑数字特性，比如倍数特性、奇偶特性、尾数法。

　　下面我们通过四个题目一起来学习不定方程的破解之法。

　　代入排除

　　【例1】设a、b均为正整数，若11a+7b=84，则a的值为：

　　A.4B.5

　　C.7D.8

　　【答案】C

　　【解析】已知11a+7b=84，求a的值，而选项中都给了可能的值，所以，可以结合选项代入验证。代入A选项，114+7b=84，得7b=40，则b不为整数，不符合题意，排除;代入B选项，115+7b=84，得7b=29，b不为整数，排除;代入C选项，117+7b=84，得7b=7，解出b=1，符合题意，故本题选C。

　　倍数特性

　　【例2】某人花400元购买了若干盒樱桃。已知甲、乙、丙三个品种的樱桃单价分别为28元/盒、32元/盒和33元/盒，问他最多购买了多少盒丙品种的樱桃?

　　A.3B.4

　　C.5D.6

　　【答案】B

　　【解析】本题设甲、乙、丙三个品种分别购买了x、y、z盒，那么由题意可知28x+32y+33z=400，三个未知量一个方程式，为不定方程。由于盒数都是正整数且28x、32y、400都是4的倍数，那么33z必然是4的倍数，即z是4的倍数，结合选项，只有B符合题意。

　　奇偶

　　特性

　　【例3】某儿童艺术培训中心有5名钢琴教师和6名拉丁舞教师，培训中心将所有的钢琴学员和拉丁舞学员共76人分别均地分给各个老师带领，刚好能够分完，且每位老师所带的学生数量都是质数。后来由于学生人数减少，培训中心只保留了4名钢琴教师和3名拉丁舞教师，但每名教师所带的学生数量不变，那么目前培训中心还剩下学员多少人?

　　A.36B.37

　　C.39D.41

　　【答案】D

　　【解析】设每名钢琴、拉丁舞老师分别带领学员x、y人，由共76人，可列不定方程5x+6y=76。观察方程式会发现，等式右边为偶数，所以等式左边5x、6y奇偶性必然相同，又因为6y确定为偶数，所以5x也为偶数，x为偶数，又由题可知x为质数，2是质数中唯一的偶数，所以x=2，y=11，即每名钢琴老师带2名学员，每名拉丁舞老师带11名学员。由所带学生数不变可得，剩余学员有4×2+3×11=41(人)。因此，选择D选项。

　　尾数法

　　【例4】超市将99个苹果装进两种包装盒，大包装盒每个装12个苹果，小包装盒每个装5个苹果，共用了十多个盒子刚好装完。问两种包装盒相差多少个?()

　　A.3B.4

　　C.7D.13

　　【答案】D

　　【解析】设大、小包装盒各有x、y个，由大盒每个装12个、小盒每个装5个，可知12x+5y=99。观察等式会发现5y的尾数很特殊，尾数只能为0或者5，由偶特性可知，12x为偶数、99为奇数，故5y为奇数，其尾数为5。此时12x尾数为9-5=4，可得x=2或x=7。代入验证，当x=2时，y=15，符合共十多个盒子，此时15-2=13;当x=7时，y=3，不符合共十多个盒子(刚好十个)。故两种包装盒相差13个。因此，选择D选项。

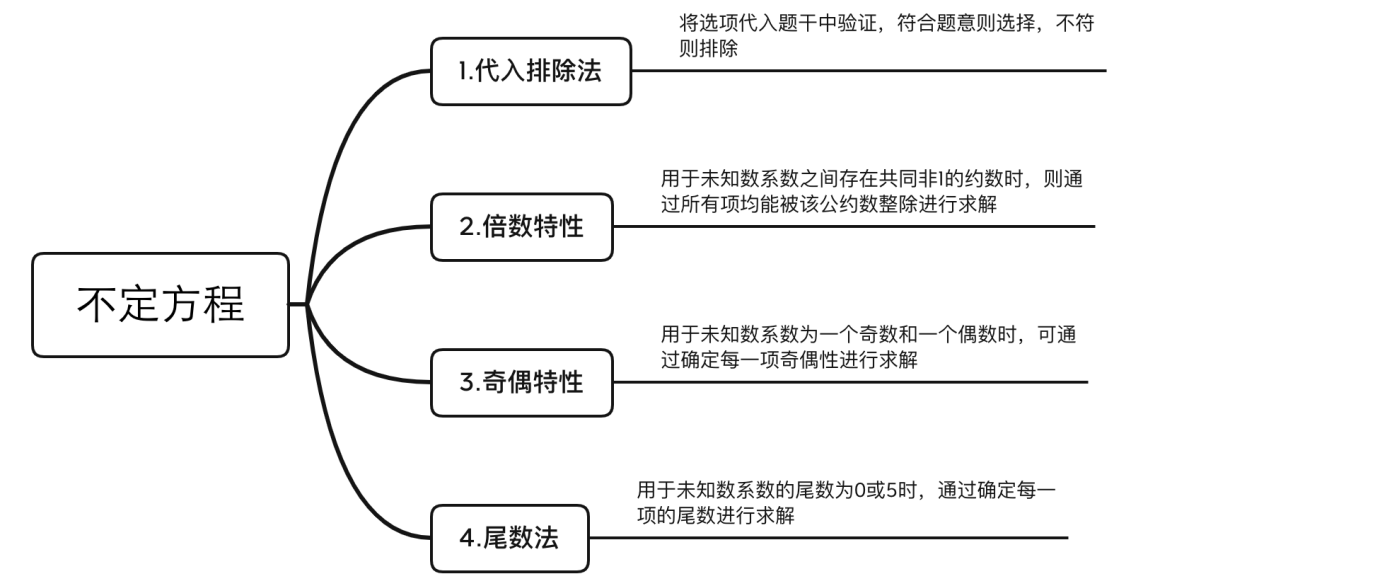
　　通过以上四个题目，向大家讲解了不定方程的解法，分析等量关系，再找出合适的方法求解，难题迎刃而解。为了更好的让各位考生掌握破题之法，我们通过以下思维导图进行总结，希望各位考生能举一反三，运用到考试当中。

　　原文标题：2023山东公务员行测数量关系之不定方程破解之法

　　文章来源：华图教育(MD5：780418808d54d760dc6831f8dce35b2c)