2023年重庆公务员行测高分技巧：数量关系中的数列构造

【导读】重庆华图为您提供：2023年重庆公务员行测高分技巧：数量关系中的数列构造，详细信息请阅读下文！如有疑问请加【2023重庆公务员上岸交流群:677564082】 ，更多重庆公务员备考指导/技巧/试题请关注重庆华图微信公众号（CQhuatu），重庆华图咨询电话：023-67518090。

推荐：2023年重庆市考公务员笔试系统提升班

推荐：2023版重庆公务员考试4本套（教材+历年）

　　数列构造是指根据题目描述的数列特征，构造一种极端情况，从而求解数列中某一项的最大值或者最小值。数列构造题目在国考数量关系题中时有出现，属于思路相对固定的题目，只要摸清它的窍门，往往可以手到擒来。那么，如何识别这种题目类型并迅速求解呢?且容我细细道来。

　　1.如何来识别数列构造题目?

　　数列构造通常是描述存在一系列数字(通常是正整数且各不相同)，告诉你这些数字的总和，要你求其中某一个的最大值或者最小值。明显的特征是它的提问通常含有两个“最”字，即“最大(小)的那个数，它的最小(大)值是多少?”

　　2.如何来进行解题?

　　我们先举一个简单的例子：有4个正整数，它们各不相同，且总和是10，求最大的那个正整数的最小值是多少?解题步骤可以简单概括为四步：排序——定位——构造——求和。

　　排序即根据题目所说有几个数按从大到小进行排序，以避免后续列式的过程中出现遗漏。这里提到有4个数，我们可以先排序①②③④。

　　定位即将要求的数设为未知数。在这里我们要求最大的那个正整数，可以设第①个数字为x。

　　构造即是根据题目条件进行反向构造。由于总和10已经固定，要求第①个的 最 小值，即相当于其他三个数都要取最大值。正整数之间至少相差1，即第 ② 个数字最大为(x-1)，第 ③ 个数字最大为(x-2)，第④个数字最大为(x-3)。

　　求和即是将所有数字加起来等于题目说的总和，列方程求解。在这道题目中，我们可以列方程：x+(x-1)+(x-2)+(x-3)=10。解方程得x=4，即最大的那个正整数的最小值是4。

　　3.例题讲解

　　【2021年国考-地市-64】某地10户贫困农户共申请扶贫小额信贷25万元已知每人申请金额都是1000元的整数倍，申请金额最高的农户申请金额不超过申请金额最低农户的2倍，且任意2户农户的申请金额都不相同，问申请金额最低的农户最少可能申请多少万元信贷?

　　A.1.5 B.1.6

　　C.1.7 D.1.8

　　【答案】B

　　【解析】第一步，排序。题目中说有“10户”，按从大到小排序10个数。

　　第二步，定位。题目问“ 申请金额最低的农户 ”，设第⑩个数是x。

　　第三步，构造。要求 申请金额最低的农户的最少值，即其它①到⑨的数要最大。题目又提到“申请金额最高的农户申请金额不超过申请金额最低农户的2倍，且任意2户农户的申请金额都不相同”，因此其它①到⑨的数如下表所示：

　　第四步，求和。注意统一单位，25万元=250千元。列方程可得：2x+(2x-1)+(2x-2)+(2x-3)+(2x-4)+(2x-5)+(2x-6)+(2x-7)+(2x-8)+x=250。化简可得19x=286，解得x≈15.05。x为最少是15.05的正整数，即x要向上取整，得x=16(千元)=1.6(万元)。

　　因此，选择B选项。

　　4 . 小结

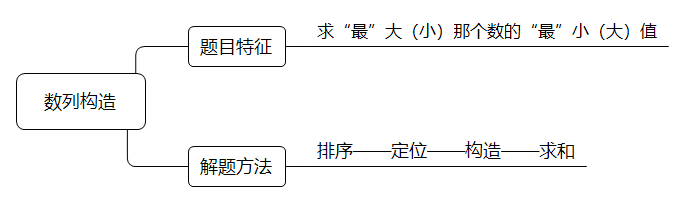
　　数量构造属于特征较为明显，解题思路相对固定的一种题型(如下思维导图所示)，在国考行测数量中是可以争取的，希望同学们能通过本文掌握此类题型 ，有效提分。

　　原文标题：2023年福建省考行测高分技巧：数量关系中的数列构造

　　文章来源：华图教育(MD5：fe393cbf09fcebb245a251973a1895fc)