2024年国家公务员考试的笔试内容是什么_国家公务员局考试网

【导读】重庆华图为您提供：2024年国家公务员考试的笔试内容是什么_国家公务员局考试网，详细信息请阅读下文！重庆华图及时为您提供2024年国家公务员招考公告、职位表、考试大纲、面试公告等相关信息，更多信息请关注重庆华图微信公众号(CQhuatu)，咨询电话：023-67159500。

　　2024国家公务员招录考试报名时间一般在什么时候呢？根据历年国家公务员公告发布时间来看，2024国考公告预计10月发布。届时华图教育将同步国家公务员考试网更新2024年国考公告、考试时间、职位表等相关考试信息，请广大考生保持关注！

　　点击查看>>>2024年国家 公务员考试公告

　　点击查询>>>2024年国家 公务员考试职位表

　　点击查看>>>国家 公务员考试历年分数线

　　一、国考笔试内容

　　公务员考试科目分为笔试和面试，笔试分为专业科目和公共科目，专业科目是部分职业要求考试的，如公安机关人民警察职位。公共科目是所有职位都要考的，分为行测(行政职业能力测验)和申论。

　　1.行测

　　公务员行测是必考的科目之一，行测主要由数量关系、语理解与表达、资料分析、判断推理、常识判断五大板块组成。

　　(1)数量关系：主要考察应试者的数据分析、推理、判断和运算的能力，比较常见的题型有数字推理、数字运算等。

　　(2)言语理解与表达：主要考察应试者的语言表达和理解能力，需要对文字材料进行分析和处理，比较常见的题型有片段阅读理解、文章阅读理解、选词填空等。

　　(3)资料分析：主要考察应试者对文字材料、图表材料的综合处理能力，比较常见的题型是图表统计、数字统计分析等开放型题目。

　　(4)判断推理：主要考察应试者的逻辑能力和推理能力，这部分通常会涉及图形、实物关系、概念理解等的内容，比较常见的题型有图形推理、类比推理、逻辑判断、定义判断等。

　　(5)常识判断：主要考察应试者对常识的掌握情况，以及对国内外重大事件的关注情况，比较常见的是开放型的题目，通常需要应试者进行自我观点的简要阐述。

　　2.申论

　　公务员申论也是必考科目之一，申论内容根据职位等级进行划分，等级分为省级以上(含副省级)和市(地)以下。

　　(1)省级以上(含副省级)综合管理类职位申论考试主要测查报考者的阅读理解能力、综合分析能力、提出和解决问题能力、文字表达能力。

　　(2)市(地)以下综合管理类和行政执法类职位申论考试主要测查报考者的阅读理解能力、贯彻执行能力、解决问题能力和文字表达能力。

　　3.专业科目

　　公务员的专业科目职位分为：人民警察专业科目考试科目、中国银保监会专业科目笔试考试科目、8个非通用语职位外语水平测试、证监会专业考试科目，每个专业科目考察侧重点会有所区别。

　　4.面试

　　国考面试一般有结构化面试、无领导小组面试、半结构化面试、结构化小组面试等;主要面试形式为结构化和无领导。

　　二、历年国考公告发布时间

　　以下为历年国家公务员公告发布时间，仅供考生备考参考。

2018-2024年国家公务员考试公告汇总
年份	公告发布时间	查看公告及职位表	报名时间	笔试时间
2024国考	？？？？	暂未公布	？？？？	？？？？
2023国考	10月24日	2023国考公告|职位表	10月25日-11月3日	12月4日
2022国考	10月14日	2022国考公告|职位表	10月15日-10月24日	11月28日
2021国考	10月14日	2021国考公告|职位表	10月15日-10月24日	11月29日
2020国考	10月14日	2020国考公告|职位表	10月15日-10月24日	11月24日
2019国考	10月21日	2019国考公告|职位表	10月22日-10月31日	12月2日
2018国考	10月28日	2018国考公告|职位表	10月30日-11月8日	12月10日

　　推荐备考>>>2024年国考《领航计划3.0》   2024年公考国庆嗨学赢

　　推荐教材>>>2024版国家公务员录用考试专用教材(行测+申论) 教材+试题 4本

　　推荐网课>>>2024年国家公务员笔试系统提升班网课

>>>公告预约-预约领取2024国考白皮书<<<

　　国家 公务员考试备考

2024年国家公务员行测备考：数量关系之最值问题应该这样备考

　　行测备考：数量关系之最值问题应该这样备考

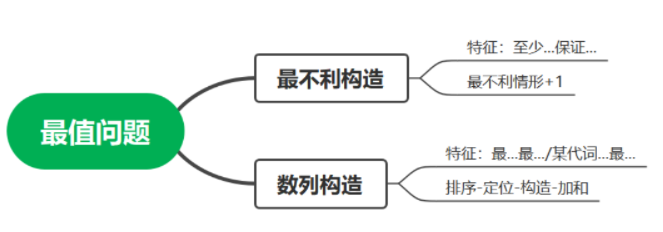
　　数量关系最值问题是公务员考试里面常考的题型之一，但是难度没有那么大，常见的最值问题包括两大题型，分别是最不利构造和数列构造。

　　题型一：看我如何搞定最不利构造

　　例1：某演唱会主办方为观众准备了白红橙黄绿蓝紫7种颜色的荧光棒各若干只，每名观众可在入口处任意选取2只，若每种颜色的荧光棒都足够多，那么至少( )名观众中，一定有两人选取的荧光棒颜色完全相同。

　　A.14

　　B.22

　　C.28

　　D.29

　　【答案】D

　　【解析】第一步，本题考查最不利构造。

　　例2：某会展中心布置会场，从花卉市场购买郁金香、月季花、牡丹花三种花卉各20盆，每盆均用纸箱打包好装车运送至会展中心，再由工人搬运至布展区。问至少要搬出多少盆花卉才能保证搬出的鲜花中一定有郁金香?

　　A. 20盆

　　B. 21盆

　　C. 40盆

　　D. 41盆

　　【答案】D

　　【解析】第一步，本题考查最值问题，属于最不利构造。 第二步，根据“至少……保证……”可知本题为最不利构造，答案为“所有最不利情况+1”。要求搬出的鲜花中一定有郁金香，最不利的情况是把所有月季花、牡丹花都搬出来，即搬出20+20=40(盆)。在此基础上再搬1盆，就能够保证搬出的鲜花中一定有郁金香，即至少要搬出40+1=41(盆)。 因此，选择D选项。

　　题型二：数列构造掌握规律也不难噢!

　　例1：从某物流园区开出6辆货车，这6辆货车的平均装货量为62吨，已知每辆货车载重量各不相同且均为整数，最重的装载了71吨，最轻的装载了54吨。问这6辆货车中装货第三重的卡车至少装载了多少吨?

　　A. 59

　　B. 60

　　C. 61

　　D. 62

　　【答案】B

　　【解析】第一步，本题考查最值问题，属于数列构造。 第二步，总和一定，求某项最值，使用数列构造的方法。首先，根据题意将6辆货车的载重量从大到小排序则第一重的为71吨，最轻的为54吨，求第三重的卡车至少载重多少，则其余货车载重尽量多，设第三重的卡车至少载重x吨，那么构造排名第二至第五的载重依次为：70，x，x-1，x-2。可列方程：71+70+x+(x-1)+(x-2)+54=62×6，解得x=60。 因此，选择B选项。

　　例2：某高校计划招聘81名博士,拟分配到13个不同的院系,假定院系A分得的博士人数比其他院系都多,那么院系A分得的博士人数至少有多少名?

　　A. 6

　　B. 7

　　C. 8

　　D. 9

　　【答案】C

　　【解析】第一步，本题考查最值问题中的数列构造问题。 第二步，总共招聘81名博士，要想院系A分得的博士数最少，则应构造其余院系分得的博士数尽可能多。设院系A分得博士x名，那么其余12个院系最多均有x-1名，可列方程：x+(x-1)×12=81，解得x≈7.2，那么院系A分得的博士至少有8名。 因此，选择C选项。

　　原文标题：2023河南省考行测备考：数量关系之最值问题应该这样备考

　　文章来源：河南华图教育(MD5：ef187fac1abe43894ea108d3c8da12f9)

（编辑：bailin01）